REFRAG: Recursive Fragmentation for Efficient Retrieval-Augmented Decoding

17 Sep, 2025

Problem Statement

Retrieval-Augmented Generation (RAG) pipelines empower LLMs by pulling external knowledge into the context window. But a fundamental issue persists:

Retrieved documents are long and redundant.
Compressing them naïvely either loses crucial details or wastes context tokens.
The challenge is preserving semantic fidelity under a strict token budget.

Mathematically: if each retrieved document $D_{j}$ is mapped into fragments $f_{j, i}$ and the LLM can only handle $B$ tokens, we want to minimize the information loss

ℰ = ‖ F - \tilde{F} ‖_{2}^{2}

where $F$ is the full set of fragment embeddings and $\tilde{F}$ is their compressed reconstruction, subject to $| \tilde{F} | \leq B$ .

This is essentially a low-rank approximation under a budget constraint.

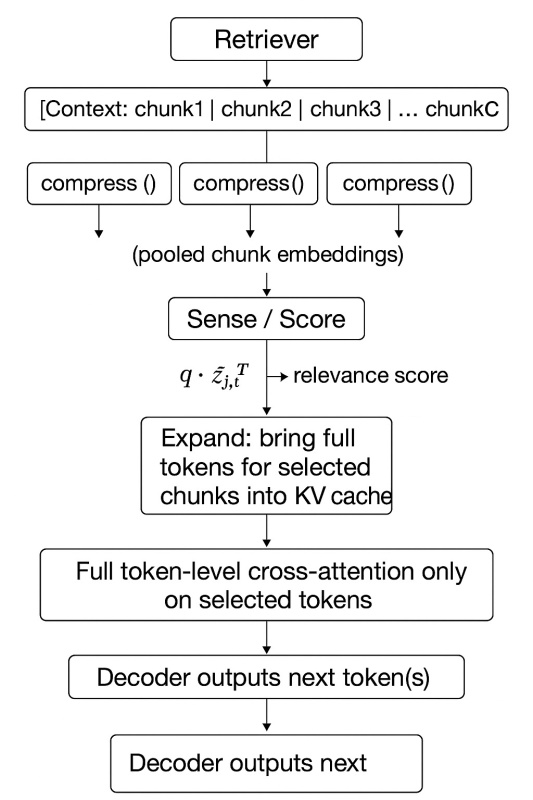
Big Idea: Fragment then Compress

Instead of compressing entire documents:

Fragment each document into semantically coherent chunks.
Compress each chunk into a small latent embedding.
Score relevance between query and compressed chunks.
Select & Expand the most promising ones back to full token detail.

This way, the model filters through compressed summaries but attends to full tokens only for the relevant few.

Mathematical Intuitions

1. Fragment Embeddings

Each fragment $f_{j, i}$ is encoded as

F_{j, i} = ϕ (f_{j, i}) \in ℝ^{d}

where $ϕ$ is a pretrained encoder.

2. Compression Mapping

We compress via linear projection:

z_{j, i} = W F_{j, i} + b, W \in ℝ^{d^{'} \times d}, d^{'} < d

Interpretation: this reduces dimension but preserves dominant variance directions.

Error bound (from matrix approximation theory):

{min}_{W} ‖ F - W^{⊤} W F ‖_{F}^{2} = \sum_{k > d^{'}} σ_{k}^{2}

where $σ_{k}$ are singular values of $F$ . So compression error is exactly the “energy” in discarded dimensions.

3. Diversity-Preserving Selection

Selecting top- $k$ fragments is not enough; we need coverage. Define objective:

{max}_{S, | S | = k} \sum_{f \in S} q^{⊤} z_{f} + λ \cdot \log det (Z_{S}^{⊤} Z_{S})

First term = relevance (dot product with query $q$ ).
Second term = diversity via determinant (DPP-style).
$λ$ trades off relevance vs. coverage.

4. Cross-Attention Expansion

After selection, expand full tokens from chosen fragments and feed to LLM with cross-attention:

H = Attention (Q, K, V), Q = W_{Q} q, K = W_{K} Z_{S}, V = W_{V} Z_{S}

This focuses LLM compute on the most relevant token spans.

The ReFrag Pipeline

blog

Complexity Analysis

Standard Full Attention

Cost: $O (n^{2} d)$ for $n$ tokens.
Memory: $O (n^{2})$ .

ReFrag Attention

Compression: $O (C d)$
Scoring: $O (n C d)$
Expansion: $O (k L d)$ , where $L$ = tokens per chunk.

Total cost:

O (n C d + k L d)

Break-even condition:
When $k ≪ C$ , ReFrag yields massive savings.

PyTorch Prototype

import torch
import torch.nn as nn

class FragmentCompressor(nn.Module):
    def __init__(self, d_in=768, d_out=128):
        super().__init__()
        self.linear = nn.Linear(d_in, d_out)
    def forward(self, x):
        return self.linear(x)

class ReFragPipeline(nn.Module):
    def __init__(self, d_in=768, d_out=128, d_model=256, n_heads=4):
        super().__init__()
        self.compressor = FragmentCompressor(d_in, d_out)
        self.cross_att = nn.MultiheadAttention(d_model, n_heads, batch_first=True)
        self.q_proj = nn.Linear(d_in, d_model)
        self.k_proj = nn.Linear(d_out, d_model)
        self.v_proj = nn.Linear(d_out, d_model)

    def forward(self, query, frags, topk=5):
        z = self.compressor(frags)              # Compress
        scores = torch.einsum('bd,bnd->bn', query, z)
        topk_idx = torch.topk(scores, k=topk, dim=1).indices
        batch_idx = torch.arange(frags.size(0)).unsqueeze(-1).expand_as(topk_idx)
        z_sel = z[batch_idx, topk_idx]         # Select top-k

        Q = self.q_proj(query).unsqueeze(1)
        K, V = self.k_proj(z_sel), self.v_proj(z_sel)
        out, _ = self.cross_att(Q, K, V)       # Cross-attend
        return out.squeeze(1)

# toy run
B, N, d_in = 2, 10, 768
frags = torch.randn(B, N, d_in)
query = torch.randn(B, d_in)
model = ReFragPipeline()
final_repr = model(query, frags)
print(final_repr.shape)

Discussion & Open Questions

Fragment granularity: How to best split documents, sliding windows or semantic boundaries?
Compression functions: Linear is simple; could autoencoders yield better trade-offs?
Adaptive budgets: Can expansion $k$ depend dynamically on query difficulty?
Diversity term optimization: Exact determinant is expensive, need efficient surrogates.

Key Takeaway

ReFrag reframes retrieval compression as a fragment-level low-rank approximation with adaptive expansion. By fragmenting, compressing, scoring, and then expanding, it preserves semantic signals at a fraction of the token cost.

In short: it’s not just about making things smaller, it’s about compressing the right fragments.