Mixture of Experts (MoE) [Theory and Implementation]

19 Aug, 2025

In this, we will learn about the MoEs and Sparse MoEs; both are mostly the same, but different in use cases. This can be used for the last-minute revision for the interviews OR learn with maths intuition...

This is not a new concept made by DeepSeek. The MoE was first coined by Prof. Geoffrey Hinton and later on used by DeepSeek tactically in the FFNs.

Paper Link: DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models

My Implementation from scratch: MoE_Implementation

Mixture of Experts Architecture

MoEs in the Large Neural Networks mixture_of_experts_architecture

MoEs in the DeepSeek moe_in_deepseek

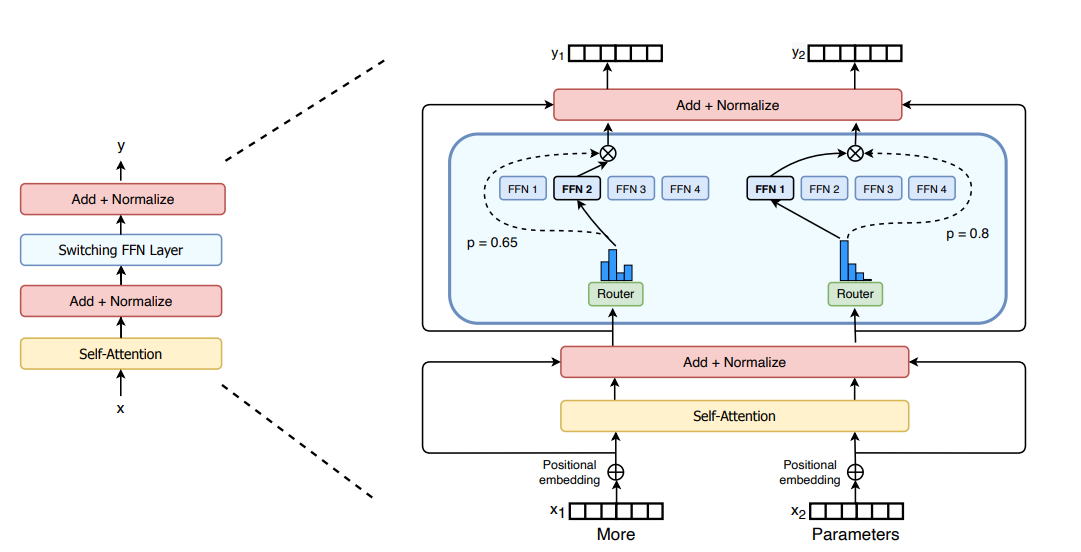
MoEs in Switch Transformer mow_in_switch_transformer

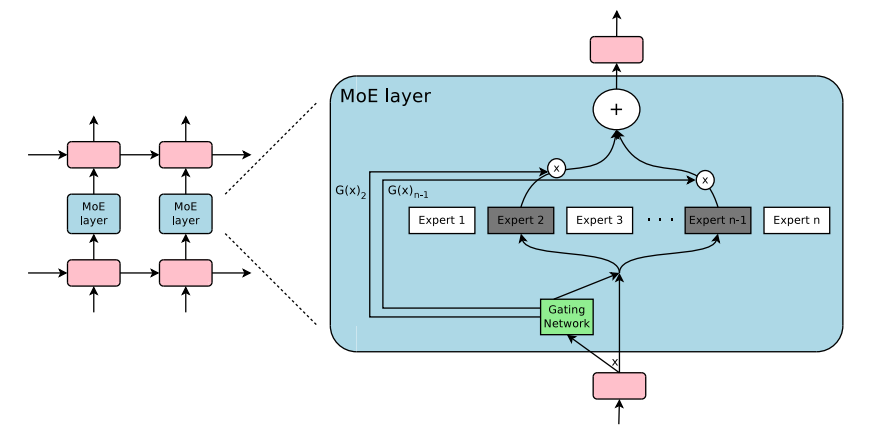
The Mixture of Experts (MoE) is a neural network architecture that uses a set of expert networks to solve tasks, while a gating network determines which experts to use for each input. Instead of using all experts for every input, the MoE model uses a sparse of experts(usually a small number) to make predictions, improving efficiency and scalability.

It is divided into three parts: Expert Networks, Gating Networks, Combination of Outputs

Important Formulas

Input: $x \in ℝ^{d}$
Expert Network Output: $y_{i} = f_{i} (x)$
Gating Network (score for expert $i$ ):
$g_{i} (x) = σ (w_{i}^{⊤} x)$ , where $σ$ is the sigmoid function
Top- $K$ Selection (by gate scores):
${g_{i_{1}} (x), g_{i_{2}} (x), \dots, g_{i_{K}} (x)}$ , where $g_{i_{j}} (x)$ are the top- $K$ values
Final MoE Output (Weighted Sum of Top- $K$ Experts):
$$ y_{\text{final}} = \sum_{k=1}^{K} g_{i_k}(x) \cdot f_{i_k}(x) $$

1. The Core Intuition of MoE

At the simplest level:

Standard neural nets: every parameter is active for every input.

MoE: only a small subset of parameters (experts) are activated depending on the input.

Think of it as a committee of specialists. A question comes in → the "gating mechanism" picks which specialists should answer → the final output is the weighted combination of their answers.

This gives:

Scalability → you can have billions of parameters but use only a fraction per input.
Specialization → different experts handle different parts of the data distribution.

2. Basic Math of MoE

Let’s formalize.

Suppose:

Input token representation: $x \in ℝ^{d}$

We have $E$ experts, each is a function $f_{i} (x)$ . For simplicity, think of each expert as an MLP layer.

The MoE layer output is:

y = \sum_{i = 1}^{E} g_{i} (x) \cdot f_{i} (x)

Where:

$f_{i} (x)$ = the output of the $i$ -th expert
$g_{i} (x)$ = gating function weight for expert $i$ (probability-like, usually from a softmax)

Gating Function:

g (x) = Softmax (W_{g} x)

Here $W_{g}$ is a learnable matrix.

In sparse MoE (most popular in practice, e.g., Switch Transformer, GLaM):

We don’t use all experts.

Instead, we select the Top-K experts (say, 1 or 2) with highest gate score.

So effectively:

y = \sum_{i \in TopK (g (x))} g_{i} (x) \cdot f_{i} (x)

3. Intuition of Mathematics

The gating mechanism is like a router that decides which expert to call.

Training encourages experts to specialize in handling different types of tokens (e.g., numbers vs. code vs. natural language).

By using Top-K, we make the computation cheap: we don’t run all experts, just a few.

Efficiency gain:

Suppose $E = 64$ experts, each with 50M parameters → 3.2B parameters total.

If we use Top-2 experts per input, the effective compute per token is ~100M parameters (instead of 3.2B).

So you get the capacity of a giant model with the compute of a smaller one.

4. Architectures of MoE

(A) Shazeer et al. (2017) – Sparsely Gated MoE

First popularized MoE for language models.
Each token routed to Top-K experts.
Introduced load balancing loss to prevent some experts from being overused.

(B) Switch Transformer (Google, 2021)

Simplification: route each token to only one expert (Top-1).
This reduces communication overhead and makes scaling easier.
Huge scaling: trained a 1.6 trillion parameter model with MoE.

Equation:

y = f_{i^{*}} (x) where i^{*} = \arg max g (x)

5. Training Challenges & Solutions

Load Imbalance:

Some experts get all tokens, others are idle.

Solution: Add auxiliary loss to encourage balanced usage.

Example:

L_{balance} = α \cdot Var (expert usage)

Routing Instability:

Gate may change suddenly → unstable learning.

Solution: Use noise, temperature scaling, or smooth routing.

Communication Overhead:

Sending tokens to multiple experts across GPUs is expensive.

Solution: Use all-to-all optimized kernels (e.g., DeepSpeed-MoE).

6. Backpropagation Derivation (Single Token, Single MoE Layer)

Setup & Notation

Input: $x \in ℝ^{d}$
Experts: $E$ experts, indexed by $i = 1, \dots, E$
Each expert is a 2-layer FFN:
- $a_{i} = W_{1, i} x + b_{1, i}$
- $s_{i} = σ (a_{i})$
- $h_{i} = W_{2, i} s_{i} + b_{2, i} = E_{i} (x)$
Router logits: $ℓ = W_{r} x + b_{r} \in ℝ^{E}$
Temperature: $τ > 0$
Softmax gate probabilities: $p = softmax (ℓ / τ)$
$p_{i} = \frac{e^{ℓ_{i} / τ}}{\sum_{j} e^{ℓ_{j} / τ}}$
Top-K (hard mask): $S = TopK (p)$
Renormalized combine weights:
$α_{i} = \frac{p_{i}}{\sum_{j \in S} p_{j}} \cdot 1 [i \in S]$
Layer output:
$y = \sum_{i \in S} α_{i} h_{i} \in ℝ^{d}$
Loss: $L = L (y)$
Upstream gradient: $g = \frac{\partial L}{\partial y} \in ℝ^{d}$

Step 1: Gradients w.r.t. Expert Outputs and Combine Weights

Since $y = \sum_{i \in S} α_{i} h_{i}$ :

For $h_{i}$ (if $i \in S$ ): $\frac{\partial L}{\partial h_{i}} = α_{i} g$
For $α_{i}$ (if $i \in S$ ): $\frac{\partial L}{\partial α_{i}} = g^{⊤} h_{i}$

Step 2: Gradients Inside Each Expert

Let $u_{i} = \frac{\partial L}{\partial h_{i}} = α_{i} g$

Then:

$\frac{\partial L}{\partial W_{2, i}} = u_{i} s_{i}^{⊤}$
$\frac{\partial L}{\partial b_{2, i}} = u_{i}$
$\frac{\partial L}{\partial s_{i}} = W_{2, i}^{⊤} u_{i}$
$\frac{\partial L}{\partial a_{i}} = (\frac{\partial L}{\partial s_{i}}) ⊙ σ^{'} (a_{i})$
$\frac{\partial L}{\partial W_{1, i}} = (\frac{\partial L}{\partial a_{i}}) x^{⊤}$
$\frac{\partial L}{\partial b_{1, i}} = \frac{\partial L}{\partial a_{i}}$

Expert contribution to input gradient:

{\frac{\partial L}{\partial x} |}_{expert i} = W_{1, i}^{⊤} ((W_{2, i}^{⊤} (α_{i} g)) ⊙ σ^{'} (a_{i}))

Only experts $i \in S$ receive/use these gradients.

Step 3: Gradients w.r.t. Masked Softmax Weights $α$

We treat $α$ as a softmax over masked logits:

z_{i} = {\begin{matrix} ℓ_{i} / τ & i \in S \\ - \infty & i \notin S \end{matrix}, α_{i} = \frac{e^{z_{i}}}{\sum_{j \in S} e^{z_{j}}} for i \in S

Softmax Jacobian (restricted to $S$ ):

\frac{\partial α_{i}}{\partial z_{j}} = α_{i} (δ_{i j} - α_{j}), i, j \in S

Chain rule to logits:

\frac{\partial α_{i}}{\partial ℓ_{j}} = \frac{1}{τ} α_{i} (δ_{i j} - α_{j}), j \in S

Then:

$\frac{\partial L}{\partial ℓ_{j}} = \sum_{i \in S} \frac{\partial L}{\partial α_{i}} \frac{\partial α_{i}}{\partial ℓ_{j}}$
$= \frac{1}{τ} \sum_{i \in S} (g^{⊤} h_{i}) α_{i} (δ_{i j} - α_{j})$
$= \frac{1}{τ} ((g^{⊤} h_{j}) α_{j} - α_{j} \sum_{i \in S} α_{i} (g^{⊤} h_{i}))$
$= \frac{1}{τ} α_{j} (g^{⊤} h_{j} - g^{⊤} y)$
$= \frac{1}{τ} α_{j} g^{⊤} (h_{j} - y), j \in S$

And $\frac{\partial L}{\partial ℓ_{j}} = 0$ for $j \notin S$ .

Why Use $δ_{i j}$ Instead of Just 1?

Softmax is multi-dimensional, not independent.

Each output depends on all logits, so the derivative is a Jacobian.

If $i = j$ (self-derivative):
$\frac{\partial α_{i}}{\partial z_{i}} = α_{i} (1 - α_{i})$
If $i \neq j$ (cross-derivative):
$\frac{\partial α_{i}}{\partial z_{j}} = - α_{i} α_{j}$

Using $δ_{i j}$ gives both in one clean formula:

\frac{\partial α_{i}}{\partial z_{j}} = α_{i} (δ_{i j} - α_{j})

Step 4: Router Gradients

Given $ℓ = W_{r} x + b_{r}$ :

$\frac{\partial L}{\partial W_{r}} = (\frac{\partial L}{\partial ℓ}) x^{⊤}$
$\frac{\partial L}{\partial b_{r}} = \frac{\partial L}{\partial ℓ}$
Router’s contribution to input gradient:

${\frac{\partial L}{\partial x} |}_{router} = W_{r}^{⊤} (\frac{\partial L}{\partial ℓ})$

Step 5: Total Input Gradient

Sum of expert and router contributions:

\frac{\partial L}{\partial x} = \sum_{i \in S} W_{1, i}^{⊤} ((W_{2, i}^{⊤} (α_{i} g)) ⊙ σ^{'} (a_{i})) + W_{r}^{⊤} (\frac{\partial L}{\partial ℓ})

7. What Interviewers Love to Probe in MoE Architectures

Who gets the gradient?

Only the selected experts (for that token) receive gradients from the main loss.
The router gets gradients only through the selected $α$ values i.e., for experts in the Top- $K$ set.
Unless you use Top-1 without scaling ("Top-1-no-scale"), the router gradient is sparse.
Auxiliary losses (like load balancing or entropy loss) are often used to improve the router training signal.

Router–Input Coupling

The input gradient includes a router path:

${\frac{\partial L}{\partial x} |}_{router} = W_{r}^{⊤} (\frac{\partial L}{\partial ℓ})$
This means the routing decisions affect not only the expert weights but also the upstream features and gradients i.e., the router is coupled with input representations.
It’s not just about deciding which expert gets used it also shapes the input representation during training.

Top-1 vs Top-K Trade-Off

Top-1 Routing (Switch Transformers):
- Only one expert per token.
- Simpler and faster.
- But: No gradient signal to the router from the main loss unless:
  - You scale the expert output by the probability $p_{i}$ .
  - Or add a strong auxiliary loss to guide the router.
Top-K Routing:
- Allows richer combinations and more robust gradients.
- Slightly more computationally expensive than Top-1.