LoRA and QLoRA: Efficient Fine-Tuning for Large Language Models

03 Aug, 2025

Training GPT-style models doesn’t just break banks; it breaks GPUs. With each new 10× scale-up in parameters, the compute bill balloons, and outright re-training or full fine-tuning becomes prohibitive. Yet practitioners still need to adapt these giant models to niche domains: medical text, legal briefs, and product catalogs, without blowing their budgets. Enter LoRA (Low-Rank Adaptation) and its quantized sibling QLoRA, a pair of techniques that let you squeeze top-notch performance out of today’s LLMs by tweaking only tiny, low-rank subspaces of their massive weight matrices. In this post, we’ll see why LoRA works so well, how QLoRA extends it with 4-bit quantization, and when you should choose one over the other

1. What is Fine-Tuning?

Pre-Training: It trains a large model(e.g., GPT, BERT) on vast unlabelled corpora to learn general representations.
Fine-Tuning: It adapts this pre-trained model to a specific downstream task by continuing gradient-based optimization on task-specific data.

So, standard fine-tuning updates all the model parameters.

For a transformer block weight matrix $𝐖 \in ℝ^{d \times k}$ , we adjust all $d \times k$ entries.
With hundreds of millions (or billions) of parameters, this is resource-intensive => Memory: Storing optimizer state for every weight, and Computation: Backpropagating through the entire network.

2. Problem with Fine-Tuning?

We must train the full network, which is computationally expensive for the average user when dealing with LLMs like BERT or GPT.
Storage requirements for the checkpoints are expensive, as we need to save the entire model on the disk for each checkpoint. If we also save the optimizer state (which we usually do, then the situation gets worse.)
If we have multiple fine-tuned models, we need to reload all the weights of the model every time we went to switch between them, which can be experienced and slow. For e.g., we may have a model fine-tuned for helping users write SQL Queries and one model for helping users write JS Code.

3. The Emergence of Low-Rank Methods

Low-rank approximation in linear algebra: any matrix $M \in ℝ^{d \times k}$ can be approximated by a product of two smaller matrices $A \in ℝ^{d \times r}$ and $B \in ℝ^{r \times k}$ when $r < min (d, k)$ :

M \approx A B, with rank (M) \leq r .

Key idea: Many weight changes during fine-tuning lie in a low-dimensional subspace.

Before LoRA, adapters (e.g., Houlsby et al., 2019) inserted small bottleneck "adapter" layers. LoRA extends this principle by directly factorizing the update to existing weights, rather than injecting new modules.

Low Rank Adaptation (LoRA)

Microsoft - AI

Paper Link: Low Rank Adaptation (LoRA)

1. LoRA’s Intuition

Keep the original pre-trained weights frozen to preserve their general knowledge.
Model the delta (change) to each weight matrix $W$ as a low-rank update:

W^{'} = W + Δ W, Δ W = A B, A \in ℝ^{d \times r}, B \in ℝ^{r \times k} .

By training only $A$ and $B$ , we optimize $r (d + k)$ parameters instead of $d \times k$ .
Often $r ≪ min (d, k)$ (e.g., $r = 4$ or $r = 8$ ), leading to orders-of-magnitude fewer trainable parameters.

2. LoRA Architecture (Module-Level View)

2.1 Transformer Block Overview

A transformer block consists of:

Multi-Head Self Attention (MHSA)

Key matrices:
- Query: $W_{q} \in ℝ^{d_{model} \times d_{k}}$
- Key: $W_{k} \in ℝ^{d_{model} \times d_{k}}$
- Value: $W_{v} \in ℝ^{d_{model} \times d_{v}}$
- Output: $W_{o} \in ℝ^{d_{v} \times d_{model}}$
Feedforward Network (FFN)

Two linear layers:
- $W_{1} \in ℝ^{d_{model} \times d_{ff}}$
- $W_{2} \in ℝ^{d_{ff} \times d_{model}}$

2.2 LoRA Modification: Only Certain Weights Get Low-Rank Updates

LoRA injects low-rank adapters into selected linear layers, typically:

Attention layers only: $W_{q}$ and $W_{v}$
(Sometimes also FFN layers, depending on the config.)

Instead of updating $W_{q}$ directly, we freeze it and add a learnable low-rank update:

W_{q}^{'} = W_{q} + Δ W_{q} = W_{q} + A_{q} B_{q}

Similarly for $W_{v}$ .

2.3 Module Architecture

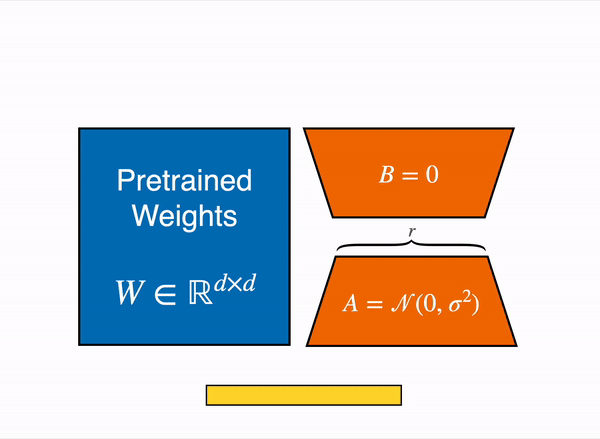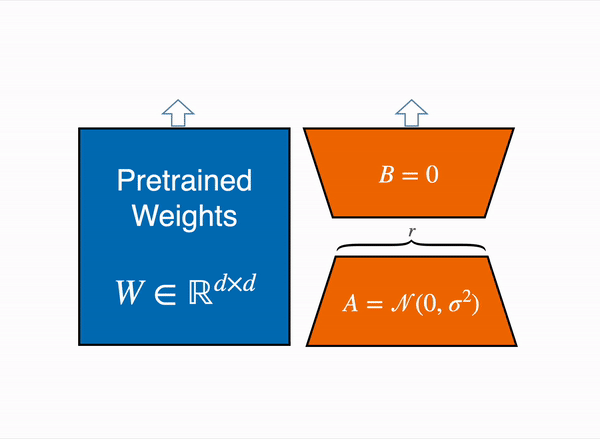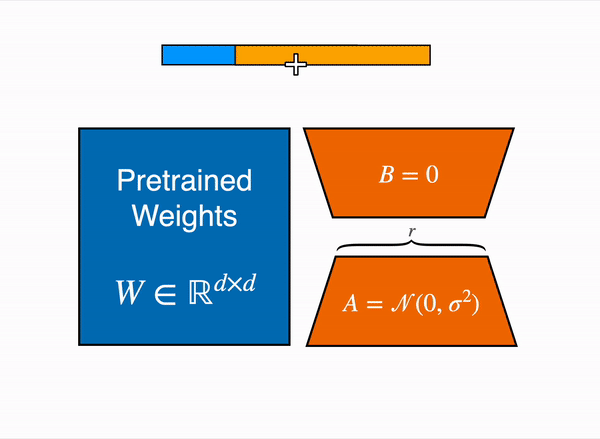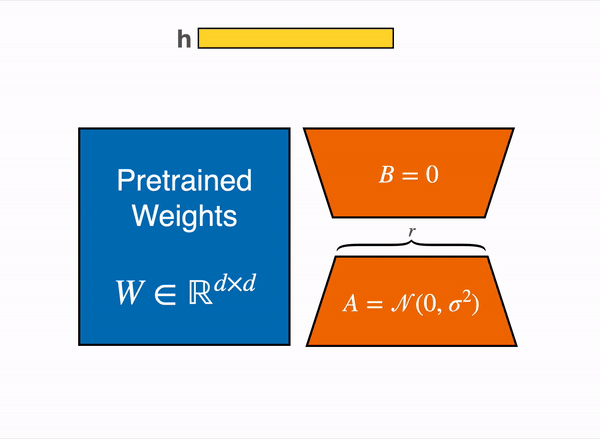
LoRA Architecture

So, Mathematically:

Output = W_{q} x + B_{q} (A_{q} x)

Here, only $𝐴_{𝑞}$ and $𝐵_{𝑞}$ are updated during training.

3. Mathematical Formulation (LoRA)

Consider a single weight matrix $W_{0} \in ℝ^{d \times k}$ in the transformer (e.g., a projection in self-attention or MLP).

Parameter Decomposition:

W^{'} = W_{0} + Δ W, Δ W = A B, A \in ℝ^{d \times r}, B \in ℝ^{r \times k} .

Forward Pass: Given input $x \in ℝ^{d}$ , the original projection yields $W_{0}^{⊤} x$ .

With LoRA:

y = W_{0}^{⊤} x + (A B)^{⊤} x = W_{0}^{⊤} x + B^{⊤} (A^{⊤} x) .

Compute $A^{⊤} x$ (size $r$ ), then $B^{⊤} (A^{⊤} x)$ (size $k$ ).

Parameter Count:
- Original: $d \times k$ .
- LoRA updates: ( $d \times r) + (r \times k$ ).
Parameter saving ratio:

\frac{d r + r k}{d k} = \frac{r k}{d k} + \frac{r d}{d k} ≪ 1 .

Training:
- Freeze $W_{0}$ (and typically the rest of the model).
- Optimize ${A, B}$ with standard gradient descent / Adam.
- Optionally, add $L_{2}$ regularization on $A$ and $B$ .
Inference: You may either:
- Dynamic sum: Keep $W_{0}$ and $A, B$ separate, computing both terms on the fly.
- Merge: Precompute $W^{'} = W_{0} + A B$ once no extra compute at inference.

4. Benefits

Less parameters to train and store: if $d$ = $1000$ , $k$ = $5000$ , then $d * k = 5, 000, 000$ , using r = 5, we get $(d * r) + (r * k) = 5000 + 25000 = 30, 000$ . Less than 1% of the original.
Less parameters = Less storage requirements
Faster backpropagation, as we don't need to evaluate the gradient for most of the parameters.
We can easily switch between two different fine-tuned models (eg, One for SQL generation and one for JS Code generation) just by changing the params of the A & B matrices instead of reloading the W matrix again.

5. Why does LoRA work

From the LoRA Paper (Section 4.1), we got:

[Section - 4.1] When adapting to a specific task, it shows that the pre-trained language models have a low "intrinsic dimension" and can still learn efficiently despite a random projection to a smaller subspace. Inspired by this, we hypothesize the updates to the weights also have a low "intrinsic rank" during adaptation.

It's basically means that the W matrix of a pretrained model contains many parameters that convey the same information as others (so they can be obtained by a combination of the other weights); This means we can get rid of them without decreasing the performance of the model. This kind of matrix is called rank-deficient (they don't have full rank).

Quantization - Low Rank Adaptation (QLoRA)

University of Washington

Paper Link: Quantization - Low Rank Adaptation (QLoRA)

'Fine-tune models with billions of parameters on a single GPU using quantization + LoRA'

1. Motivation

LoRA made fine-tuning efficient by reducing trainable parameters. However, model weights were still stored in full precision (FP32 or BF16), consuming a lot of GPU memory.

For example: LLaMA- $65$ B with full precision = $130 +$ GB VRAM

Even if only LoRA weights are trained, the frozen base model still consumes a huge memory footprint. Enter QLoRA, which quantizes the frozen weights (e.g., to 4-bit) and combines this with LoRA for maximum memory efficiency.

2. Core Idea

QLoRA = Quantized base model (4-bit) + Low-Rank Adapters (LoRA layers)

Key innovations:

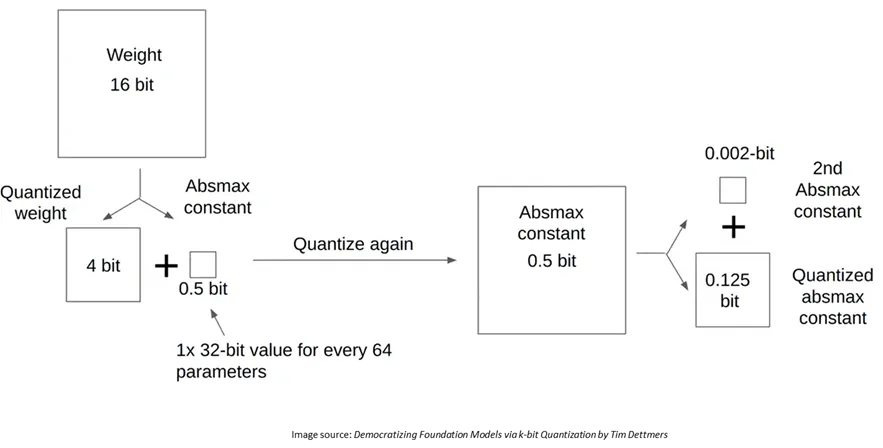
Quantize the base model weights to 4-bit using NF4 quantization (non-uniform).
Keep LoRA adapters in full precision (FP16/BF16) for learning capacity.
Use Double Quantization + Paged Optimizer to fit models on a single 24GB GPU.

3. Architecture Overview

Frozen Quantized Base
- All model weights $𝑊$ are quantized to 4-bit (using NF4 or FP4).
- These quantized weights are not updated during training.
Full-Precision LoRA Adapters
- Inserted on top of quantized layers (e.g., $𝑊_{𝑞}$ , $𝑊_{𝑣}$ , sometimes MLP layers).
- Trainable low-rank adapters $A \in ℝ^{d \times r}, B \in ℝ^{r \times k}$ .
Memory-Efficient Optimizer
- Use PagedAdamW: optimizer that pages memory in and out using CPU and GPU intelligently.
- Supports massive models like LLaMA-65B on 1 GPU.

4. Mathematical View

4-Bit Quantization of Frozen Base

Given a pre-trained weight matrix $W \in ℝ^{d \times k}$ , apply:

4.1 NF4 Quantization:

Non-uniform quantization scheme learned from the data distribution:

Q (W) = {Quantize}_{NF4} (W)

Notes:

NF4 provides better accuracy than uniform 4-bit quantization.
Weights are stored as 4-bit integers plus scaling factors (applied group-wise).

4.2 During Forward Pass:

y = Q (W) \cdot x + B^{⊤} (A^{⊤} x)

Note:

$Q (W)$ : Quantized frozen base weights
$A$ , $B$ : Full-precision LoRA adapters

5. Architecture

QLoRA Architecture

Training and Inference: LoRA vs QLoRA

Aspect	LoRA	QLoRA
Base Model Weights	Stored in full precision (FP32 / BF16)	Quantized to 4-bit (NF4 or FP4)
Trainable Parameters	Only the low-rank matrices $A \in ℝ^{d \times r}$ , $B \in ℝ^{r \times k}$	Same as LoRA: only LoRA adapters $A, B$ are trained
Frozen Weights Format	FP16 / FP32	4-bit integer quantized with separate scaling factors (group-wise NF4)
Backward Pass Through Base	No gradients through base weights	No gradients through base weights (also quantized, so not differentiable)
Memory Usage (GPU RAM)	Moderate (due to full-precision base model)	Very low (quantized base + LoRA weights in FP16)
Precision of LoRA adapters	Typically FP16 or BF16	Same: FP16 or BF16
Optimizer Used	Adam / AdamW	PagedAdamW: memory-paged optimizer for CPU+GPU hybrid optimization
Compute Requirement	Moderate to high (if base model is large)	Very low: QLoRA can fine-tune 65B models on a single A100 48GB GPU
Training Speed	Faster than full fine-tuning	Slightly slower than LoRA due to dequantization overhead during forward pass
Forward Computation	$W x + B^{⊤} (A^{⊤} x)$ with $W$ in FP16	$Q (W) x + B^{⊤} (A^{⊤} x)$ with $Q (W)$ : dequantized 4-bit base weight
Inference Model Size	Base model + LoRA adapters (~1% additional)	Quantized base model + small LoRA adapters (~0.5% additional)
Merging for Deployment	Can merge $W^{'} = W + A B$ to single matrix	More complex: requires dequantizing, summing, then re-quantizing to 4-bit
Multi-Task Adaptability	Easy — multiple adapters per task	Same — multiple low-rank adapters, each task shares the same 4-bit base
Downstream Performance	Often matches or exceeds full fine-tuning	Matches LoRA and full fine-tuning in most benchmark tasks

🙏 Thanks for Reading

Thanks for reading this deep dive into LoRA and QLoRA. I hope this gave you a clear mathematical and architectural understanding of how modern parameter-efficient fine-tuning works, and how it’s enabling powerful large language models to be adapted with minimal compute. Whether you're experimenting on a personal GPU or scaling multi-task deployments, these techniques are paving the way for more democratized AI.